Learn how you can Unlock Limitless Customer Lifetime Value with CleverTap’s All-in-One Customer Engagement Platform.
This is the first part in the Series on Tricks and Tips for Feature Engineering. In this part, we will broadly discuss some tricks and follow it up with concrete examples and detailed explanations in ensuing parts.
Predictive modeling is a formula that transforms a list of input fields or variables into some output of interest. Feature Engineering is simply a thoughtful creation of new input fields from existing input fields in an automated fashion or manually with valuable inputs from domain expertise, logical reasoning, or intuition. The new input fields could result in better inferences and insights from data and could exponentially increase the performance of predictive models.
Let’s consider an analogy to explain the various stages of an Analytics project.
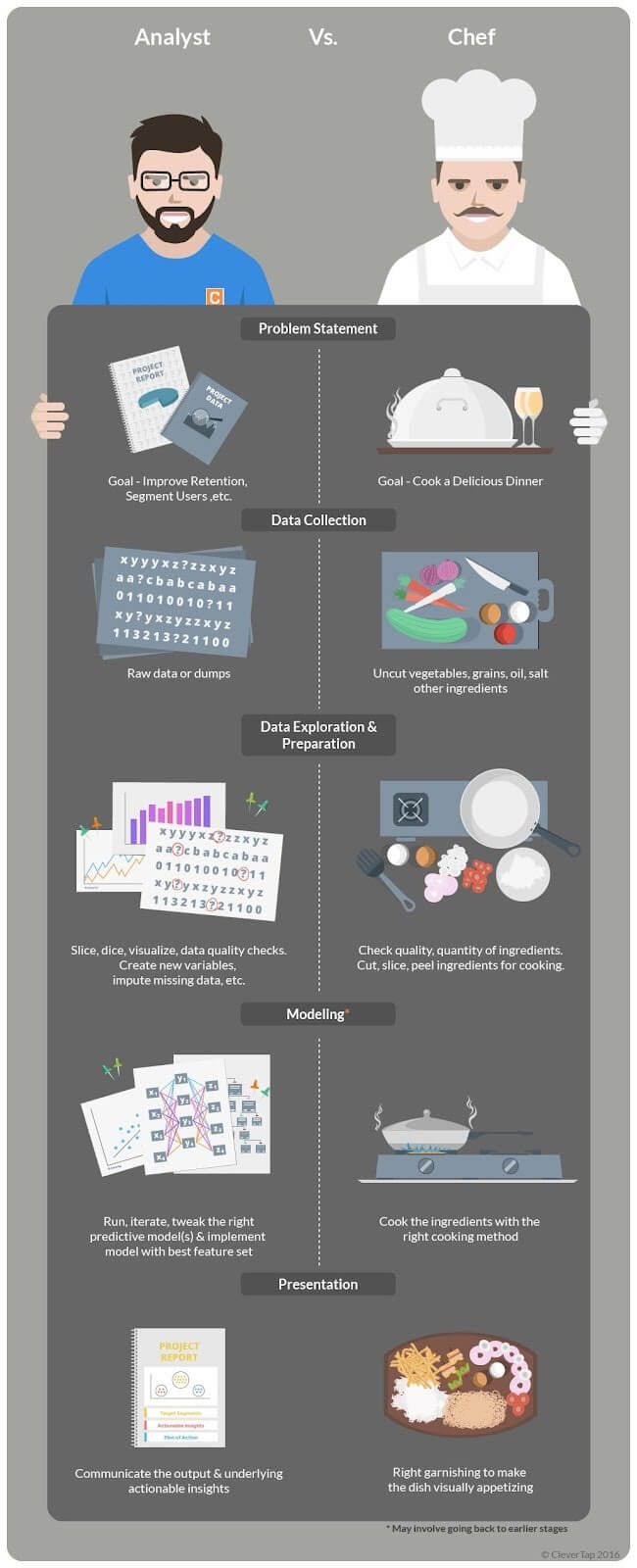
Feature Engineering is one of the most important parts of the Data Preparation process, where deriving new and meaningful variables takes place. Feature Engineering enhances and enriches the ingredients needed for creating a robust model. Many a time, it is the key differentiator between an average and a good model.
Some of the common and popular tricks employed for Feature Engineering are discussed below:
Numerical variables in your dataset are generally on different scales like height, weight, etc. To bring these variables on the same scale, it is advisable to standardize them.
A good example of standardization is the Body Mass Index (BMI), which is a popular index to check if a person is underweight or overweight by taking the weight and standardizing it with the help of the height so that the BMIs of different persons are comparable.
Failure to standardize variables might result in the algorithms giving undue higher weightage to variables that are on a larger scale, especially true for many machine learning algorithms like SVM, neural network, K-means, etc. One of the ways to standardize a variable is to take the difference of each observation from the mean of the variable and divide such difference by the standard deviation of the variable (z-score).
A contrary example where standardization is not advisable is for well-defined attributes like latitude and longitude, where one might lose valuable information due to standardization. Hence, the indiscriminate use of standardization is not advisable.
Feature binning is a popular feature engineering technique for numerical variables. It bins numerical variables based on certain techniques ranging from approaches based on simple percentile, domain knowledge, and visualization to predictive techniques. It helps you get a quick segmentation for better interpretability of the numerical variables. Creating different models for each bin could build a more specific, relevant, and accurate model for predictive models like Regression models.
A common example is grades awarded to students based on their marks, which segments the students and makes interpretation a lot easier.
We might often come across a scenario where a categorical variable has many attribute levels, like the branches of a bank, postal codes, or products listed on an e-commerce website or app. Handling many attributes or levels might become cumbersome, and looking at the frequency distribution might reveal that only a subset of such levels account for 90%-95% of the observations. Building a predictive model without treating the levels will most likely lead to a less robust model and computational efficiency will also be negatively impacted.
For example, a decision tree or random forest will tend to give more importance to the categorical variable with many levels, even though it may not deserve it. We can treat such categorical variables with predictive modeling techniques, domain expertise or even a simple frequency distribution approach might help.
Normally distributed data is needed to use a number of statistical analysis tools and techniques.
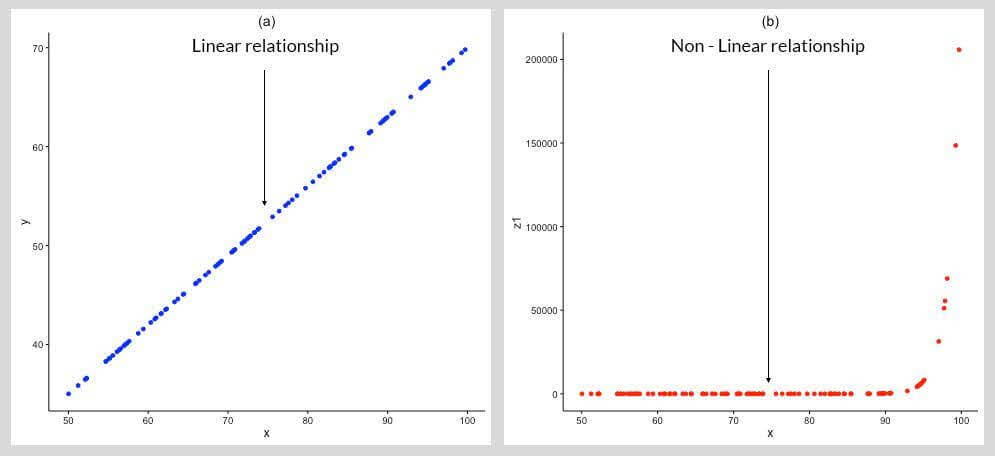
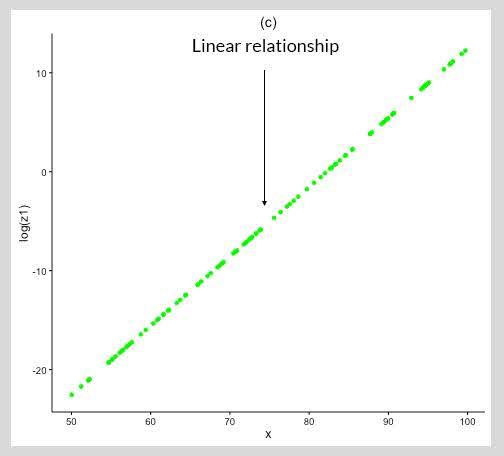
In (c) above, the variable ‘z1’ is converted to a Normal Distribution by taking the log of the variable, which converts the relationship of ‘x’ and ‘z1’ to linear from non-linear, as shown in (b). Log transformation, though useful, is not guaranteed to work all the time. One can use other transformations like taking the square root, cube root, etc. But, experimenting with various combinations is not an ideal solution.
To change the distribution of variables from non-normal to normal or near normal, Box-Cox transformations are very useful. It helps you to get the value/parameter (Log in the above case), using which the distribution of the variables can be transformed to a normal distribution.
Missing Data is a reality that any analyst has to painfully reckon with. It may make utmost sense to deal with such missing values before making any inference or building a predictive model, thereby affecting the inferences and actionable insights for a data-driven strategy. Imagine the implications of leaving out mandatory information while filing tax return statements.
Normally, you will be faced with a situation where the Categorical variables have more than 2 levels/attributes.
For example, Operating system with levels such as “iOS”, “Android” and “Windows”. You could encode them as 0, 1, and 2, respectively, for a Regression model since it requires numerical variables as inputs. In such a case, you are assigning some sort of order to the OS. But, the distance between the encoded attributes like ‘2’ (Windows) minus ‘0’ (iOS) doesn’t mean anything. Hence, creating dummy variables is necessary to ‘trick’ the algorithm into correctly analyzing attribute variables.
Instead of storing the information about different OS in one variable, you could create different variables for different OS. Each of these new variables will have only 2 levels representing the existence or its non-existence in the observation. The number of dummy variables so created will be one less than the number of levels, else it would lead to redundant information. In the above case, it is sufficient to create a dummy variable for ‘Android’ and ‘iOS’, and if the observation indicates the absence of ‘Android’ and ‘iOS’, it implies that ‘Windows’ is present.
Dummy variables could clearly lead to better predictive models since you would get a different coefficient or multiplier factor for each level and not suffer from assuming any order in the attribute/levels in the categorical variable.
Suppose you are the Credit Officer and have been given the historical data related to Income Level (‘High’, ‘Low’), the quantum of Loans already held at the time of the application and the current status of the loan (Default or Good) of the applicants post disbursal of the loan. Your goal is to create a model that will predict if a new applicant will default on a loan.
You could create a Regression model to predict the prospective defaulter with the independent variables of Income Level and quantum of Previous Loans held. This model will give you insights into how the probability of default is moving with different levels of income and previous loans.
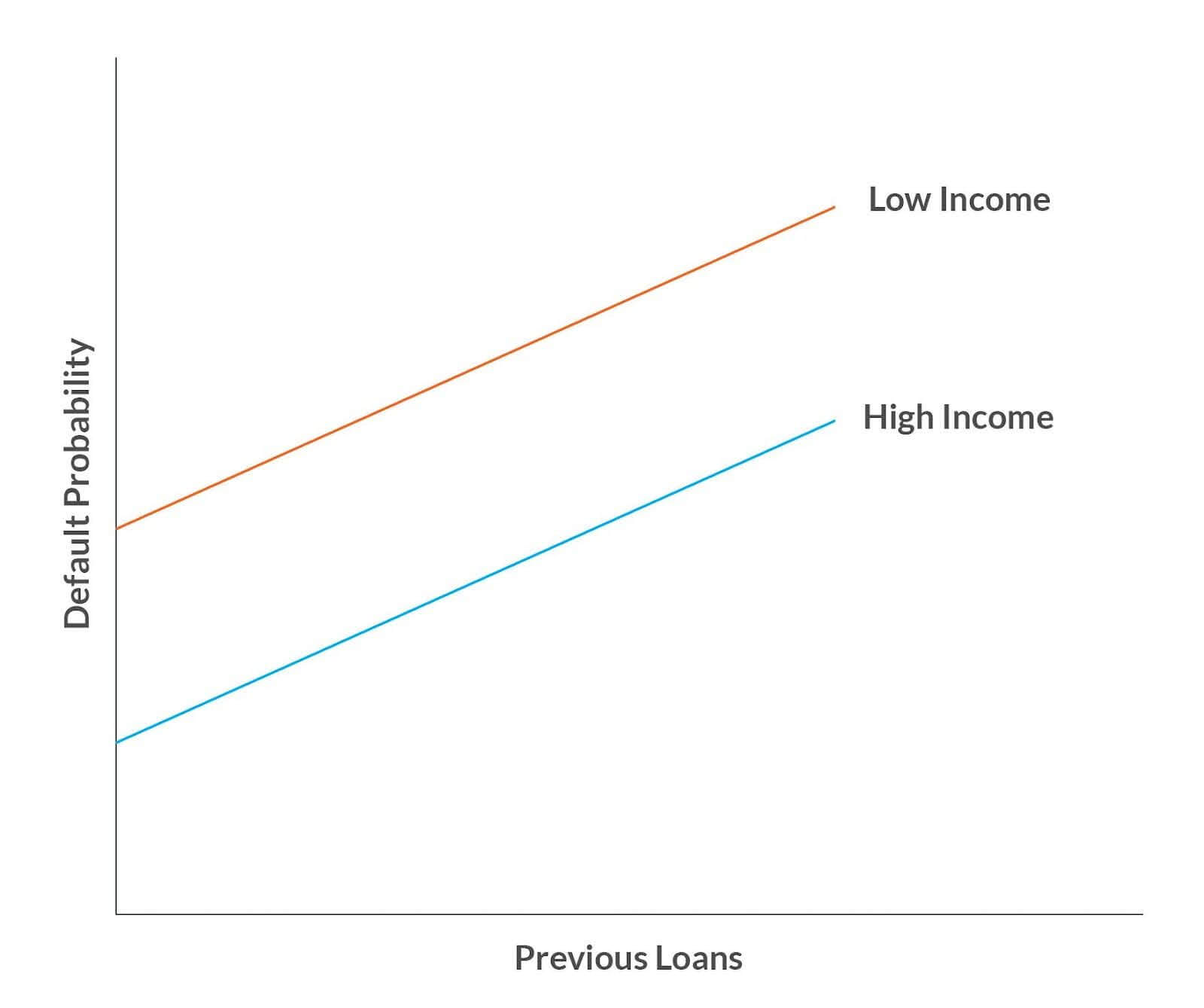
The slope of the graph reveals that the rate of increase in default probability for both Income levels is the same. The relationship between the variables is additive, i.e., the effect of Income levels on Default probability does not depend on Previous Loans held, and the effect of Previous Loans held on Default Probability does not depend on Income Level. This seems counter-intuitive as one would guess that the combination of both Income level and Previous loans held should affect Default Probability.
Let’s create a new variable in the form of an interaction variable by combining Income Level and Previous Loans (Income Level x Previous Loans).
From the slope of the above graph, one could infer that default probability increases more rapidly for applicants with Low income than High income. Thus, the model has improved with the creation of an interaction variable.
Reducing dimensionality involves reducing the amount of resources required to describe a large set of data. Suppose you have 1000 predictor variables, and there is a likelihood of high correlation among the variables, due to which you might require only a subset of predictor variables. Additionally, using all the predictor variables might result in overfitting.
Suppose a dataset consists of variables like height in inches and height in cm. In this case, it makes sense to use either height measured in inches or cms. Another dataset could consist of variables like length, breadth, and area in the same units, but here, we don’t need area since the area is a product of length and breadth.
The techniques chosen for reducing dimensionality depend on the type of variables. You would employ different methods for text, image, and numerical variables. Some of the popular techniques are to use hand-engineered feature extraction methods (e.g., SIFT, VLAD, HOG, GIST, LBP), and another stream is to learn features that are discriminative in the given context (e.g., Sparse Coding, Auto Encoders, Restricted Boltzmann Machines, PCA, ICA, K-means).
Based on the available raw data, additional and intuitive features could be created manually or automatically. In the case of text data, you might run an automated algorithm to create features like the length of the word, number of vowels, n-gram, etc. Automation is also true for deriving features for video and image files. You might also deal with the data manually, which might require domain expertise, common sense, or intuition.
As an analyst, you are trying to discover the signal from the noise. In this age of big data, the noise is most likely to increase. It is imperative that you have at least a candle to guard against the darkness. With the prudent and judicious use of all or some of the tools mentioned above, you will be equipped with more than just a candle.
Stay tuned to deep dive into each trick in the ensuing parts.
