This post in intended to help readers to understand the algorithm behind our recommendation engine. We use Collaborative Filtering (CF) to power our recommendation engine. Though there are many CF algorithms, we chose item2vec, which is based on the popular word2vec algorithm, primarily used for Natural Language Processing (NLP).
What is NLP?
Computers understand programming language that is precise, unambiguous and highly structured. Human speech, however, is not always precise — it is often ambiguous and the linguistic structure can depend on many complex variables, including slang, regional dialects, and social context. Natural Language Processing (NLP) is focused on enabling computers to understand and process human languages.
How often do you use search engines in a day? If you feel you depend a lot on search engines like Google, then you are kind of dependent on NLP as well.
When you type a few words into the search box, you immediately prompted with a lot of relevant options to auto complete your search. This is just one of many applications of NLP in our daily lives, other examples include auto-completing words, language translation, and more.
NLP uses word embeddings to map words or phrases from a vocabulary into some mathematical form, or vectors. This representation has two important and advantageous properties:
- Dimensionality Reduction: It is a more efficient representation.
- Contextual Similarity: It is a more expressive representation.
Don’t scratch your head. Things will become clearer shortly.
We chose one particular NLP technique to recommend relevant products.
Why We Chose Word2vec as the NLP Technique
Word2vec is an NLP technique that produces word embeddings.
Say you’re given sentences such as:
- Beijing is China’s capital city
- Madrid, Spain’s central capital, is a city of elegant boulevards
- Tokyo is the enormous and wealthy capital city of Japan
A cursory glance at the three sentences above reveals a pattern around city, capital and their country names going together. Likewise, extending this to multiple similar sentences such as the above can yield the relationship shown below: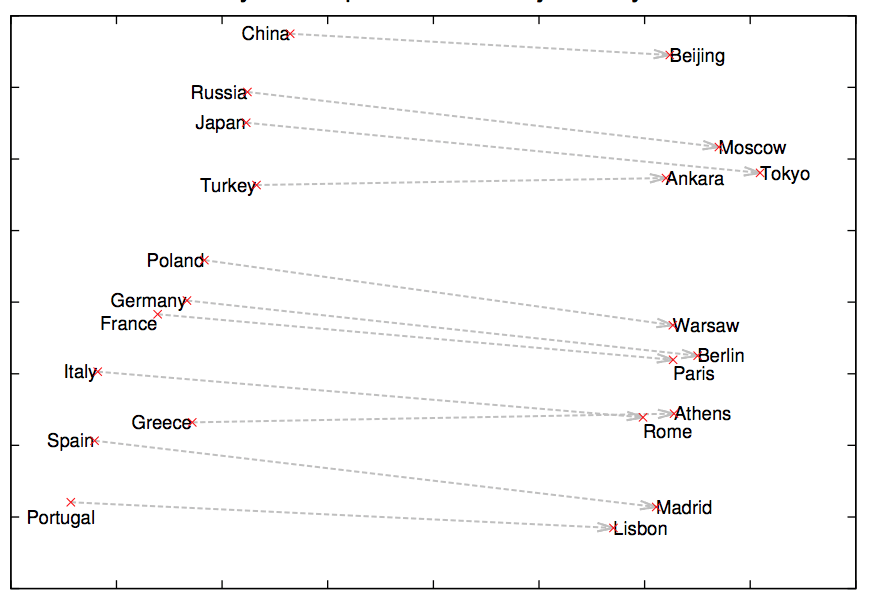
Word2vec is a shallow neural network that trains sentences to learn patterns by turning words into mathematical objects. This mathematical object, commonly known as a vector, has size (magnitude) and direction, shown as arrows above. Since we have vectors, we can now perform mathematical operations such as addition, subtraction, or measure similarity between them.
Word2vec gained popularity by being able to transform words into vectors and come up with mathematical operations like these:
- King – Man + Woman = Queen
- Moscow – Russia + France = Paris
If word2vec is able to capture this contextual information from sentences, why can’t it be extended to user behavior, where sentences could represent the items the user has purchased/viewed?
This is exactly what item2vec, the word2vec variant we use, does.
Using item2vec, we arrange user purchases into sentences, maintaining the sequences of items purchased, and then use a neural network to transform those item sequences into vectors/mathematical objects. Now it is possible to conduct mathematical operations on the items in the sequence to find similar items to recommend.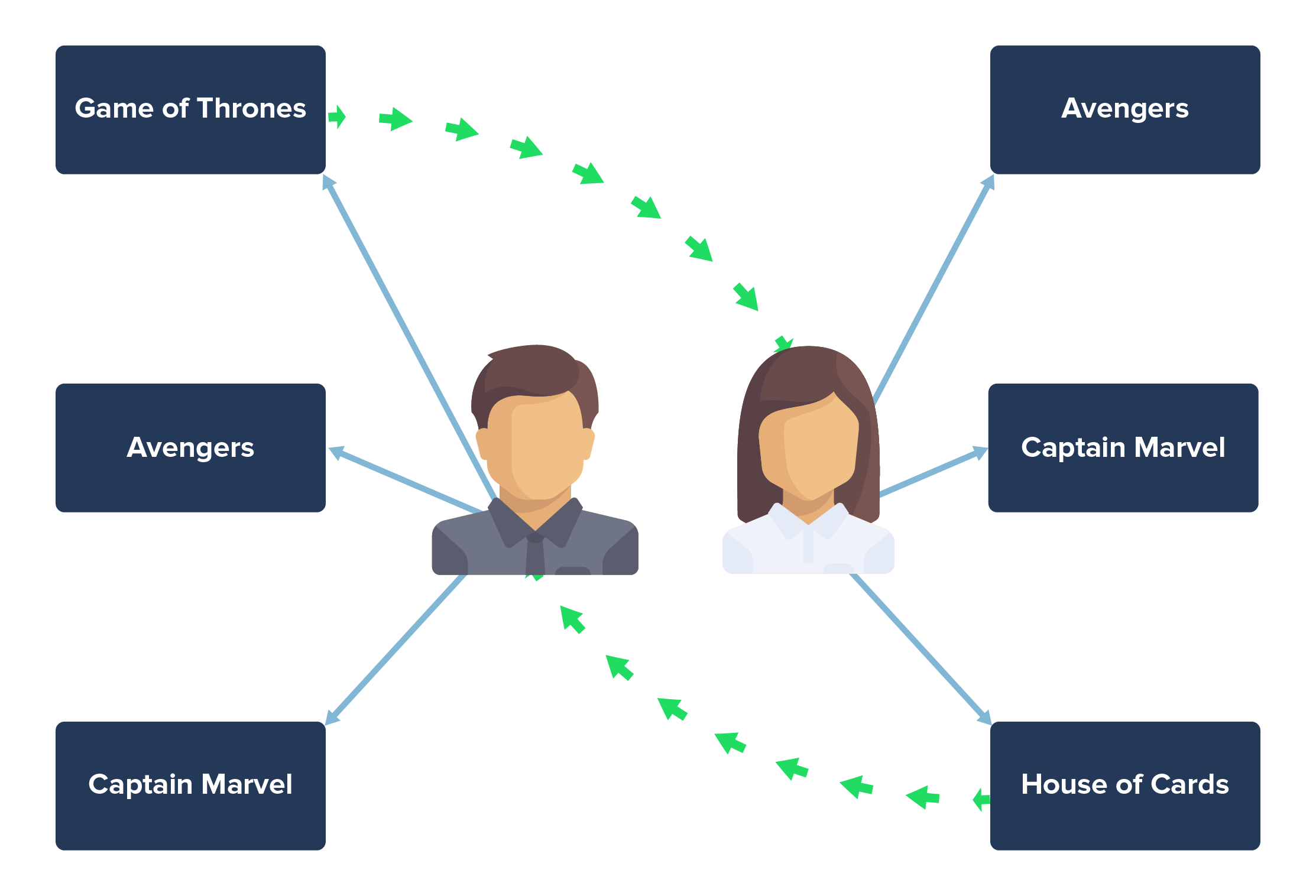
- User A’s past watched history can be represented as [Game of Thrones, Avengers, Captain Marvel].
- User B’s past watched history can be represented as [Avengers, Captain Marvel, House of Cards].
To get there, we do 4 things:
- Create a training set from the historical user purchase item sequences. The training set consists of pairs of a single item input and a related item output.
- Turn these items from strings into numerical representations called vectors.
- Feed the vectorized training set into a Neural Network, which helps us optimize the size of the vector representations.
- Use the optimized vector representations to determine similarity between items by calculating their mathematical closeness/similarity using techniques like pearson correlation and cosine similarity.
We can then rank our item recommendations accordingly.
To create the training set, we generate our input-output pairs from items that are next to each other in the items sequences we have generated. For example:
| Item Sequence | Training Input – Output Pairs | |||
|---|---|---|---|---|
| Game of Thrones | Avengers | Captain Marvel | → | (Game of Thrones, Avengers) |
| Game of Thrones | Avengers | Captain Marvel | → | (Game of Thrones, Avengers) (Avengers, Captain Marvel) |
|---|
| Game of Thrones | Avengers | Captain Marvel | → | (Captain Marvel, Avengers) |
|---|
| Avengers | Captain Marvel | House of Cards | → | (Avengers, Captain Marvel) |
|---|
| Avengers | Captain Marvel | House of Cards | → | (Captain Marvel, Avengers) (Captain Marvel, House of Cards) |
|---|
| Avengers | Captain Marvel | House of Cards | → | (House of Cards, Captain Marvel) |
|---|
Likewise, we can create the training dataset in a similar manner for other users. If in the dataset, we get more cases of (Avengers, Captain Marvel) than (Captain Marvel, House of Cards), then the probability of pairing Captain Marvel with Avengers would be higher than House of Cards.
Because machine learning algorithms don’t understands strings, and can only deal with numerical inputs and outputs, we then need to convert the input-output pairs in the training
dataset into numerical representations before we feed them to our neural network.
To do that, let’s assume, we have a library of 10 movies and series in total.
| Serial Number | Item |
|---|---|
| 1 | Avengers: Infinity War |
| 2 | Black Panther |
| 3 | House of Cards |
| 4 | Captain Marvel |
| 5 | Game of Thrones |
| 6 | Incredibles 2 |
| 7 | Deadpool 2 |
| 8 | Mission Impossible – Fallout |
| 9 | Venom |
| 10 | The Grinch |
Then, for example, let’s take the input-output pairs where Avengers is the input. These are:
(Avengers, Game of Thrones)
(Avengers, Captain Marvel)
In the above example, Avengers is the input and the outputs are Game of Thrones and Captain Marvel.
Now we can use the fact that we have 10 total items in the library to encode each input/output string into a numerical data structure called a vector. Each item can now be represented by placing a 1 in the vector position corresponding to its serial number in our item catalog.
Since Avengers is the first item in the table, it is marked as 1 in the vector in the first position and other items as 0. Note the length of the vector is 10 which is equal to the total number of rows in the input table.
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|
Game of Thrones and House of Cards are in the 4th and 5th row respectively in the table and correspondingly, shown in the 4th and 5th positions in the vector as 1.
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
|---|
Likewise, we can represent the items watched by other users in the form of vectors rather than strings.
If you observe closely, there are 0’s in most of the places. Imagine a case where your library is in tens of thousands. Mathematically, it is difficult to bring out the relationship between vectors where majority of the elements are 0’s. Hence, we have to use neural networks to tell us the optimal size the vector representations can be reduced to without losing predictive accuracy. (And if you’re feeling a bit lost on neural networks, I previously wrote about the inner workings of a neural network.).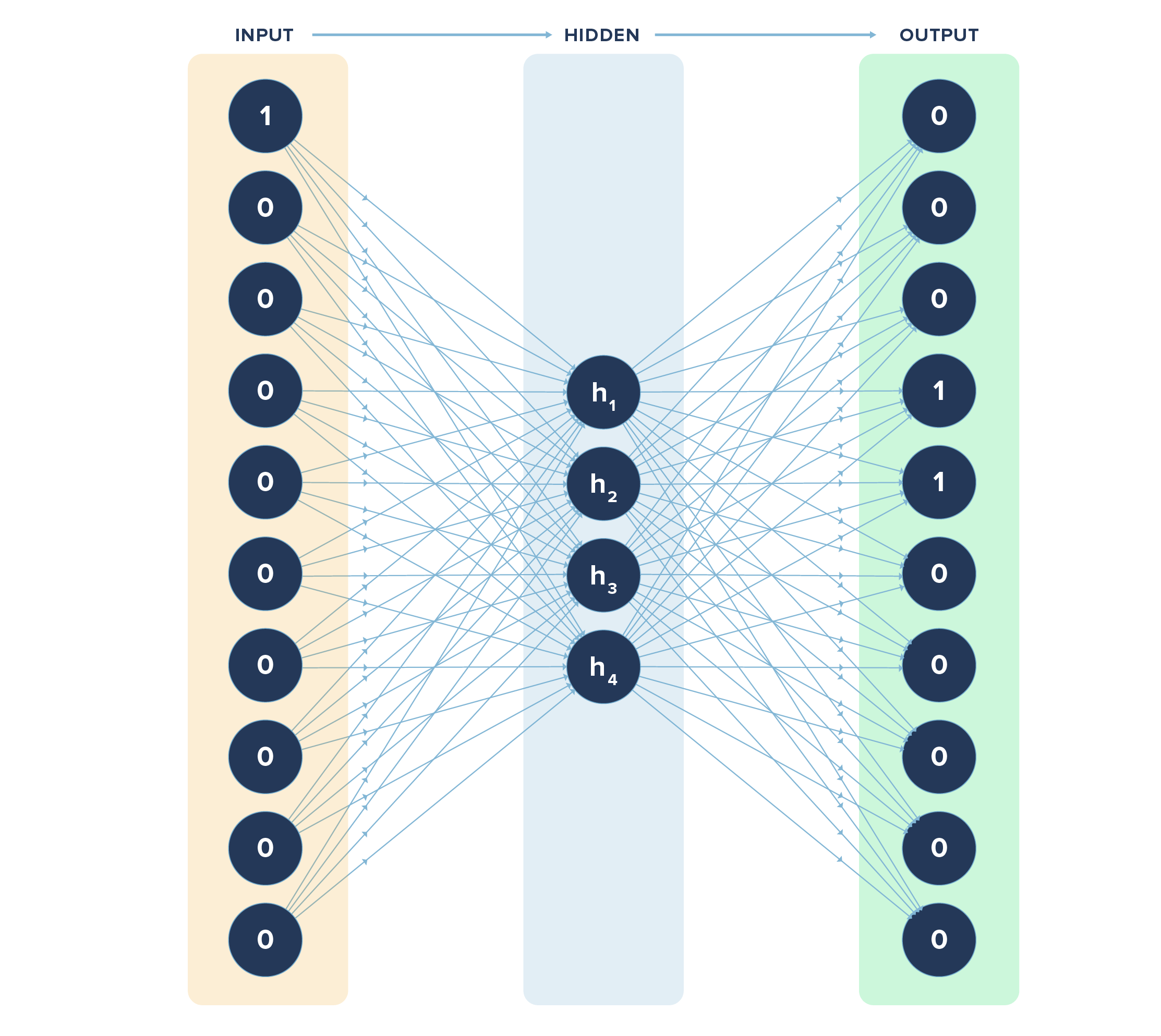
In the above neural network, we fed the input vector (length 10) and got the output vector (length 10), the values of which are known. What we learnt from the neural network is the values in the hidden layer of length 4 that gives us the same predictive accuracy as using a vector of length 10, markedly improving computational time and expense without sacrificing accuracy.
Optimization: Do You Need the Entire Vector Stored?
Earlier in this article, we said that dimensionality reduction is one of the benefits of the word embeddings. The job of the hidden layer is to come up with the item/word embeddings. So instead of defining each item as a vector of length 10, now we can just use a vector of length 4 to describe an item. It is a lot shorter representation.
In a library of 10 items, this hardly makes a difference. But, imagine a library of thousands of movies and series. What if you can express such high dimensional representation consisting of thousands of items in say, 50 or 100?
.
Another way to look at is, do you need the entire vector to be stored? Instead of the movie, can we decide to just store whether the item is a Superhero movie, a Political movie, a Marvel or Non-Marvel movie? In that case, instead of a vector of length 10, we can store the information for each item in the vector of length 4.
This is a simplistic explanation. But in reality, the catalog size will be much higher as will the optimal dimension size generated by our neural network. In practice, we have achieved excellent results with hidden layer dimensions of the order of 300 and lower given catalog sizes in the hundreds of thousands..
Now that we have the optimally reduced input dimension size, we can efficiently calculate similarities between the vector representations using techniques like pearson correlation, and cosine similarity. We can then rank our recommendations according to the calculated similarities.
Conclusion
In this post, we got a bird’s eye view of the algorithm that powers our recommender system. We will cover more about the thought process behind the need for a recommender engine in our next post. Stay tuned!
Jacob Joseph 
Heads Data Science.Expert in AI, Data & Analytics and awarded 40 under 40 Data Scientists in India.
Free Customer Engagement Guides
Join our newsletter for actionable tips and proven strategies to grow your business and engage your customers.