In the earlier part, we discussed tricks (iv) to (vii) for feature engineering. In this part, we will dive deep into tricks (viii) and (ix). The examples discussed in this article can be reproduced with the source code and datasets available here. Refer to Part 1 for an introduction to the tricks dealt with in detail here.
viii) Reducing Dimensionality
As an analyst, you savor the scenario where you have a lot of data. But, with a lot of data comes the added complexity to analyze and make better sense of such data. Often, the variables within the data are correlated, and analysis or models built on such untreated data may lead to poor analysis or lead to a model that overfits.
It is a common practice among analysts to employ dimension reduction techniques to create new variables that number less than the original variables to explain the dataset. For example, Assume a dataset has 1000 variables, but with the dimension reduction technique, only 50 newly created variables were able to explain the original data quite well.
Dimension Reduction techniques are heavily used in image processing, video processing, and generally, where you deal with very high number of variables. You may use hand-engineered feature extraction methods like SIFT, VLAD, HOG, GIST, and LBP or learn features that are discriminative in the given context like PCA, ICA, Sparse Coding, Auto Encoders, Restricted Boltzmann Machines, etc.
In this article, we look at a popular technique called Principal Component Analysis (PCA). PCA is a technique used to emphasize variation and bring out strong patterns in a dataset.
Let’s explore PCA visually in 2 dimensions before proceeding toward a multidimensional dataset.
2D Example
Consider we have the following dataset:
Dataset
| Physics | Maths |
|---|---|
| 70 | 69 |
| 40 | 55.8 |
| 80.5 | 74.2 |
| 72.1 | 70 |
| 55.1 | 63 |
| 60 | 59.5 |
| 85.5 | 75 |
| 56 | 62 |
The dataset contains the average marks in Physics and Maths of 8 students
From the above scatter plot, it seems that there is a positive relationship between the marks in Physics and Maths.
But what if we want to summarize the above data on just one coordinate instead of two? We have 2 options:
- Take all the values of Physics and plot them on a line
- Take all the values of Maths and plot it on a line
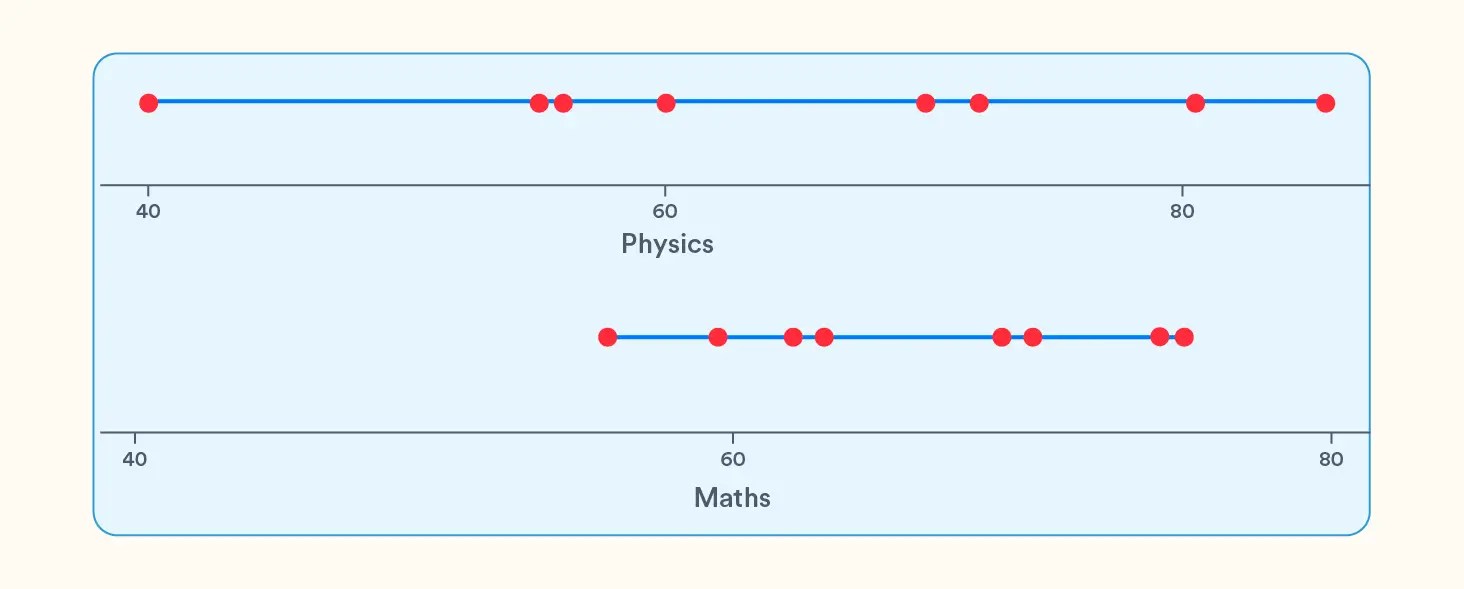
It seems the variation for marks in Physics is more than in Maths. What if we choose the Physics marks to be representative of the dataset since it varies more than Maths marks and anyway, the marks in Physics and Maths both move together? But intuitively, that doesn’t seem right. Though we chose the variable that had the maximum variation in the dataset, i.e., Physics marks, we are sacrificing the information about Maths marks totally.
Why can’t we create new variables, which take a linear combination of the existing variables and then look at such newly created variables that maximize such variation?
Transformed
| PC1 | PC2 |
|---|---|
| 0.574378 | 0.058681 |
| -2.364742 | 0.153077 |
| 1.665568 | 0.088140 |
| 0.788306 | 0.060262 |
| -0.825473 | 0.165476 |
| -0.954877 | -0.459403 |
| 2.004565 | -0.078450 |
| -0.887725 | 0.012218 |
The dataset is a transformed version of the dataset containing the marks. It is calculated by taking the principal components of the data.
Principal components are essentially linear combinations of the variables, i.e., both PC1 and PC2 are linear combinations of variables in Physics and Maths. For the 2 variables, we got 2 principal components.
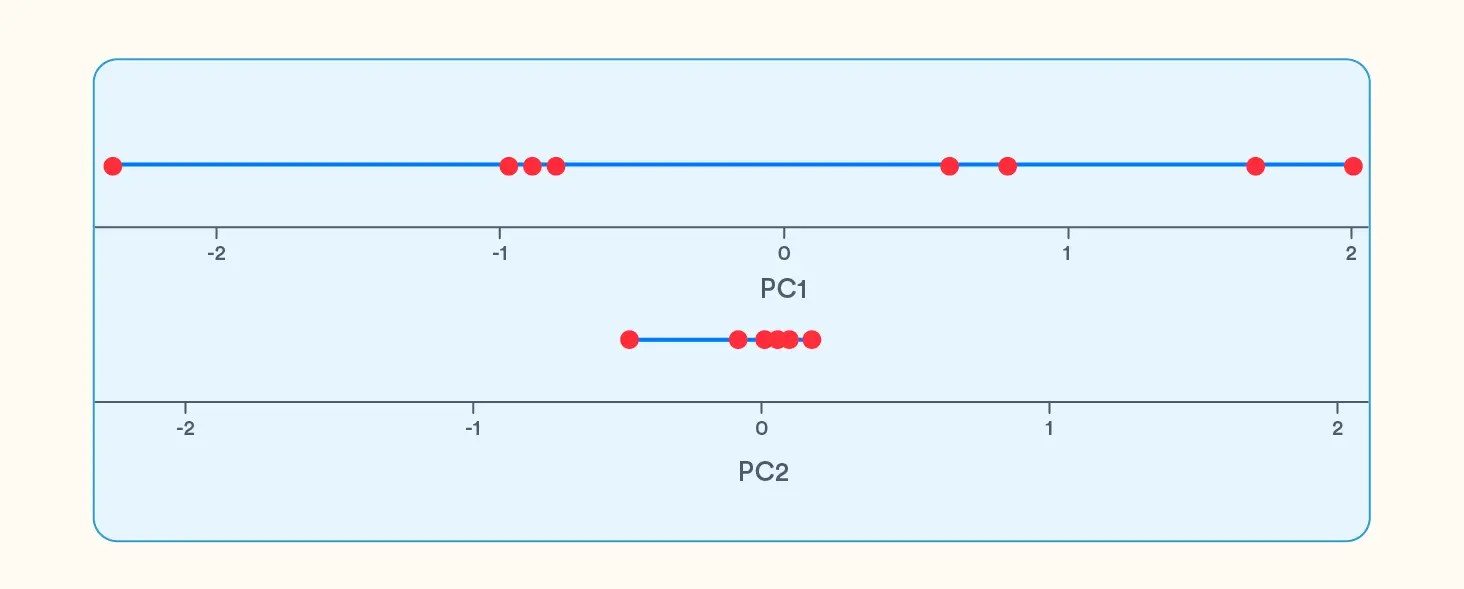
From the above line graphs, we see that PC1 shows the maximum variation, and since it is a representation of both the original variables, it is a better candidate to represent the dataset than just Physics.
Let’s observe the variance explained by both the components
Importance of Components
| PC1 | PC2 | |
|---|---|---|
| Standard Deviation | 1.402 | 0.188 |
| Proportion of Variance | 0.982 | 0.018 |
| Cumulative Proportion | 0.982 | 1.000 |
It is further clear from the above table that PC1 accounts for 98% of the variance in the dataset, and it could be used to represent the dataset.
Multidimensional Example
Let’s extend this same idea to a multi-dimensional scenario. We will try to understand with the help of the wine dataset discussed in part 2 under trick (i). To recollect, the wine dataset contains the results of a chemical analysis of wines grown in a specific area of Italy. Three types of wine are represented in the 178 samples, with the results of 13 chemical analyses recorded for each sample. The sample data set is below:
First 10 Rows
| Type | Alcohol | Malic | Ash | Alcalinity | Magnesium | Phenols | Flavanoids | Nonflavanoids | Proanthocyanins | Color | Hue | Dilution | Proline |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 14.23 | 1.71 | 2.43 | 15.6 | 127 | 2.8 | 3.06 | 0.28 | 2.29 | 5.64 | 1.04 | 3.92 | 1065 |
| 1 | 13.2 | 1.78 | 2.14 | 11.2 | 100 | 2.65 | 2.76 | 0.26 | 1.28 | 4.38 | 1.05 | 3.4 | 1050 |
| 1 | 13.16 | 2.36 | 2.67 | 18.6 | 101 | 2.8 | 3.24 | 0.3 | 2.81 | 5.68 | 1.03 | 3.17 | 1185 |
| 1 | 14.37 | 1.95 | 2.5 | 16.8 | 113 | 3.85 | 3.49 | 0.24 | 2.18 | 7.8 | 0.86 | 3.45 | 1480 |
| 1 | 13.24 | 2.59 | 2.87 | 21 | 118 | 2.8 | 2.69 | 0.39 | 1.82 | 4.32 | 1.04 | 2.93 | 735 |
| 1 | 14.2 | 1.76 | 2.45 | 15.2 | 112 | 3.27 | 3.39 | 0.34 | 1.97 | 6.75 | 1.05 | 2.85 | 1450 |
| 1 | 14.39 | 1.87 | 2.45 | 14.6 | 96 | 2.5 | 2.52 | 0.3 | 1.98 | 5.25 | 1.02 | 3.58 | 1290 |
| 1 | 14.06 | 2.15 | 2.61 | 17.6 | 121 | 2.6 | 2.51 | 0.31 | 1.25 | 5.05 | 1.06 | 3.58 | 1295 |
| 1 | 14.83 | 1.64 | 2.17 | 14 | 97 | 2.8 | 2.98 | 0.29 | 1.98 | 5.2 | 1.08 | 2.85 | 1045 |
| 1 | 13.86 | 1.35 | 2.27 | 16 | 98 | 2.98 | 3.15 | 0.22 | 1.85 | 7.22 | 1.01 | 3.55 | 1045 |

We have a total of 13 numerical variables on which we can conduct PCA analysis (PCA can run on numerical variables only). Let’s check the variable importance after running the PCA algorithm and select the principal components based on the variation in the dataset it explains.
Importance of Components
| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | |
|---|---|---|---|---|---|---|---|
| Standard Deviation | 2.169 | 1.580 | 1.203 | 0.959 | 0.924 | 0.801 | 0.742 |
| Proportion of Variance | 0.362 | 0.192 | 0.111 | 0.071 | 0.066 | 0.049 | 0.042 |
| Cumulative Proportion | 0.362 | 0.554 | 0.665 | 0.736 | 0.802 | 0.851 | 0.893 |
| PC8 | PC9 | PC10 | PC11 | PC12 | PC13 | |
|---|---|---|---|---|---|---|
| Standard Deviation | 0.590 | 0.537 | 0.501 | 0.475 | 0.411 | 0.322 |
| Proportion of Variance | 0.027 | 0.022 | 0.019 | 0.017 | 0.013 | 0.008 |
| Cumulative Proportion | 0.920 | 0.942 | 0.962 | 0.979 | 0.992 | 1.000 |
Based on the above table, it seems that more than 50% of the variance in the data is explained by the top 2 principal components, 80% by the top 5 principal components, and over 90% by the top 8.
Let’s further understand the relationship between the variables and confirm if the PCA has been able to capture the pattern in the data among the variables with the help of a biplot.
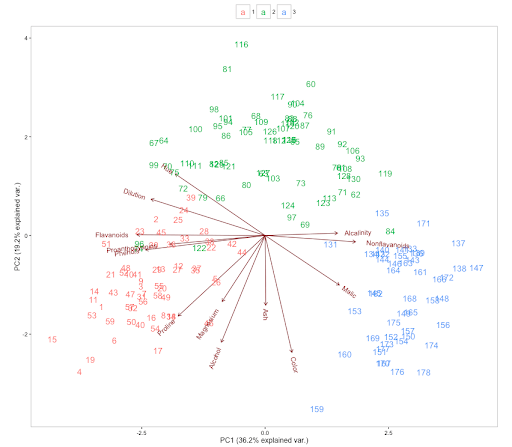
Biplots are the primary visualization tool for PCA. The biplots plot the transformed data as points shown in the form of the row index of the dataset and the original variables as vectors (arrows) on the same graph. It also helps us visualize the relationship between the variables themselves.
The direction of the vectors, length, and the angle between the vectors all have a meaning. Let’s look at the angle between the vectors. The smaller the angles between the vectors, the more the variables are positively correlated. In the above plot, if we pick a few variables, Alcalinity and Nonflavanoids have a high positive correlation due to the small angle between the vectors. The same can be said for Proanthocyanins and Phenois. Malic and Hue or Alcalinity and Phenois are negatively correlated as the vectors go in the opposite direction.
We can verify the claims by choosing the row indices from the plot.
Let’s choose row index 131 and 140
| Alcalinity | Nonflavanoids | |
|---|---|---|
| 131 | 18 | 0.21 |
| 140 | 24 | 0.53 |
Both Alcalinity and Nonflavanoids moved together
Let’s choose row index 23 and 33
| Proanthocyanins | Phenois | |
|---|---|---|
| 51 | 2.91 | 2.72 |
| 33 | 1.97 | 2.42 |
Both Proanthocyanins and Phenois moved together
Interestingly, the data points seem to form clusters indicated by the different colors corresponding to the type of wine. PCA can be useful not only for reducing the dimensionality of the dataset but also for clustering. Since we would be using only a subset of the principal components that explain the majority of the variation in the dataset while building the predictive models, it could be very useful in reducing the menace of overfitting.
ix) Intuitive & Additional Features
Sometimes, you may create additional features, which could be the result of domain knowledge and common sense either manually or programmatically.
Examples:
- How many times have you come across a dataset that contains the birth date of a user? Are you using that information in the given form, or are you transforming and creating a new variable like the Age of the user?
- You would also have come across date and time stamps that contain the information on date, hour, minutes up to seconds, if not more. Would you be taking this information as it is? Wouldn’t it be useful if new variables like the month of the year, day of the week, and hour of the day were created?
- Many businesses are seasonal in nature, while some are not. Based on the nature of the industry, a new variable recognizing the seasonality could be created.
Conclusion
The steps preceding the predictive modeling stage take up as much as 80% of an analyst’s time of which Data Preparation takes up a lion’s share. The importance of Feature Engineering in Data Preparation can’t be underestimated. If done the right way, it could lead to better insights and more efficient and robust models. The tricks discussed in the article series attempt to arm the analyst with enough ammunition in the form of tricks/tips.
Jacob Joseph 
Heads Data Science.Expert in AI, Data & Analytics and awarded 40 under 40 Data Scientists in India.
Free Customer Engagement Guides
Join our newsletter for actionable tips and proven strategies to grow your business and engage your customers.