How to remove duplicates in large datasets

Dealing with large datasets is often daunting. With limited computing resources, particularly memory, it can be challenging to perform even basic tasks like counting distinct elements, membership check, filtering duplicate elements, finding minimum, maximum, top-n elements, or set operations like union, intersection, similarity and so on.
Probabilistic data structures to the rescue
Probabilistic data structures can come in pretty handy in these cases, in that they dramatically reduce memory requirements, while still providing acceptable accuracy. Moreover, you get time efficiencies, as lookups (and adds) rely on multiple independent hash functions, which can be parallelized. We use structures like Bloom filters, MinHash, Count-min sketch, HyperLogLog extensively to solve a variety of problems. One fairly straightforward example is presented below.
The problem
We manage mobile push notifications for our customers, and one of the things we need to guard against is sending multiple notifications to the same user for the same campaign. Push notifications are routed to individual devices/users based on push notification tokens generated by the mobile platforms. Because of their size (anywhere from 32b to 4kb), it’s non-performant for us to index push tokens or use them as the primary user key.
On certain mobile platforms, when a user uninstalls and subsequently re-installs the same app, we lose our primary user key and create a new user profile for that device. Typically, in that case, the mobile platform will generate a new push notification token for that user on the reinstall. However, that is not always guaranteed. So, in a small number of cases we can end up with multiple user records in our system having the same push notification token.
As a result, to prevent sending multiple notifications to the same user for the same campaign, we need to filter for a relatively small number of duplicate push tokens from a total dataset that runs from hundreds of millions to billions of records. To give you a sense of proportion, the memory required to filter just 100 Million push tokens is 100M * 256 = 25 GB!
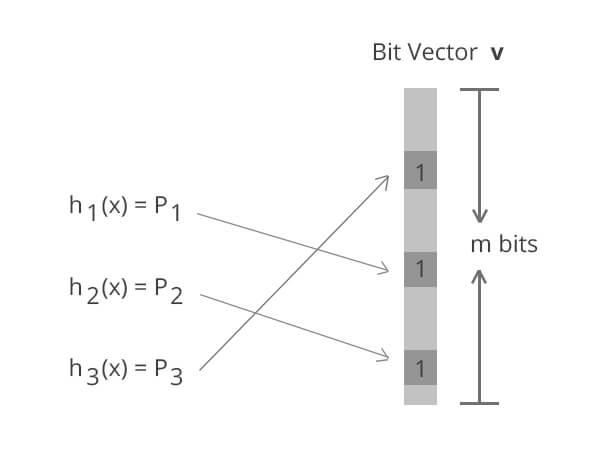
The solution – Bloom filter
The idea is very simple.

• Allocate a bit array of size $latex m $
• Choose $latex k $ independent hash functions  $latex h_i(x) $  whose range is $latex [ 0 .. m-1 ] $
• For each data element, compute hashes and turn on bits
• For membership query $latex q $, apply hashes and check if all the corresponding bits are ‘on’

Note that bits might be turned ‘on’ by hash collisions leading to false positives i,e a non-existing element may be reported to exist and the goal is to minimise this.
On hash functions
Hash functions for Bloom filter should be independent and uniformly distributed. Cryptographic hashes like MD5 or SHA-1 are not good choices for performance reasons. Some of the suitable fast hashes are MurmurHash, FNV hashes and Jenkin’s Hashes.
We use MurmurHash –

• It’s fast – 10x faster than MD5
• Good distribution – passes chi-squared test for uniformity
• Avalanche effect – sensitive to even slightest input changes
• Independent enough

Sizing the Bloom filter
Sizing the bit array involves choosing optimal number of hash functions to minimise false-positive probability.
With $latex m$ bits, $latex k$ hash functions and $latex n$ elements, the false positive probability i,e the probability of all the corresponding $latex k$ bits are ‘on’ falsely when the element doesn’t exist
$latex p = ( 1 – [ 1 – \frac{1}{m}]^{kn} )^k \approx ( 1 – e^{-\frac{kn}{m}})^k $
for given $latex m, n $, optimal k that minimises $latex p $
i,e $latex \frac{dp}{dk} = 0 \implies k = \frac{m}{n}ln(2)$
$latex \implies m = -\frac{nln(p)}{(ln(2))^2} $
so, for 100 Million push tokens with 0.001 error probability
$latex m = -\frac{100000000*ln(0.001)}{(ln(2))^2} = 171 MB $
This is significant improvement from 25 GB.