In the earlier part, we discussed tricks (i) through (iii) for feature engineering. In this part we will deep dive in trick (iv) to (vii). The examples discussed in this article can be reproduced with the source code and datasets available here. Refer to part 1 for an introduction to the tricks dealt with in detail here.
iv) Transforming Non-Normal distribution to Normal
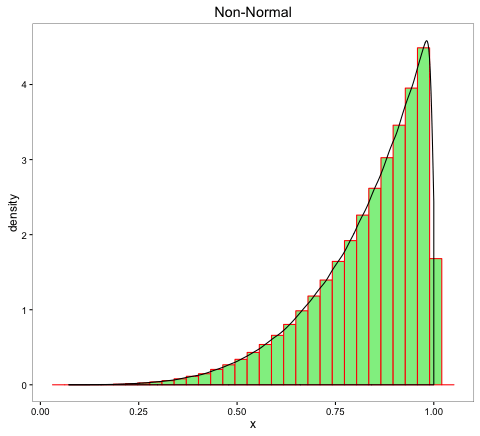
A number of statistical analysis tools and techniques require normally distributed data. Many times, we may need to treat data to transform its distribution to normal from non-normal. There are a number of techniques ranging from statistical tests to visual approaches to check if the data is normally distributed. We shall use the histogram, which is an easy visual approach to check for normality.
- (a)
- (b)
- (c)
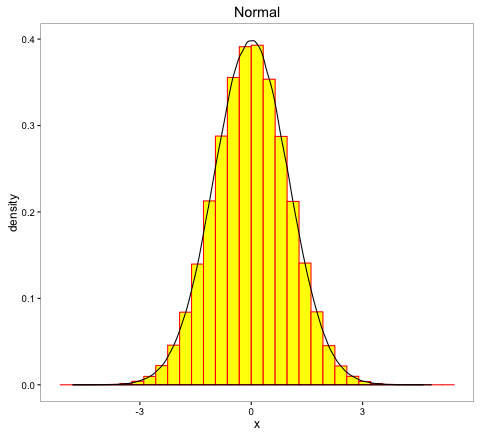
A quick way to identify normal distribution is when the histogram of the data resembles a bell. Figure (a) could be indicative of normal distribution since its histogram resembles a bell compared to figures (b) and (c).
Some of the ways to transform the distribution of the data involve taking its log or square root or cube root, etc. However, iterating over all possible transformations could be extremely time-consuming. In such cases, Box-Cox transformation could be the best bet.
Box-Cox
Statisticians George Box and David Cox developed a procedure to identify an appropriate exponent (Lambda = λ) to use to transform data into a “normal shape.”
z= x-1 where λ ≠0
z=log x where λ=0
The Lambda value indicates the power to which all data should be raised to transform it to normal. In order to do this, the Box-Cox power transformation searches from Lambda = -5 to Lambda = +5 until the best value is found.
Let’s look at an example to build a linear regression model with a dataset with 50 observations:
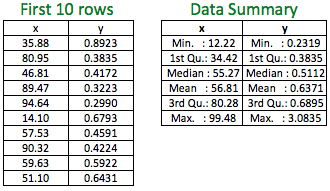
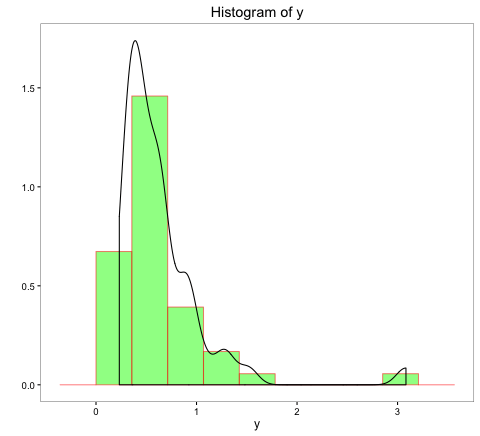
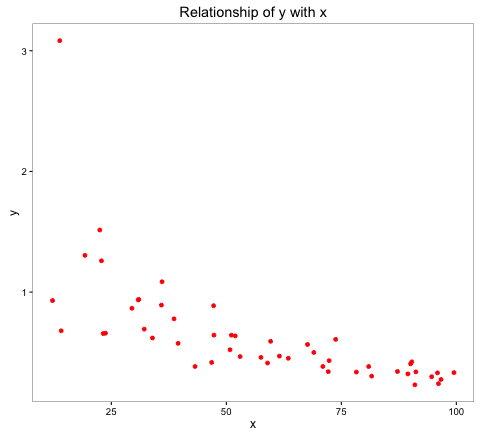
The above histogram of y indicates a non-normal distribution. The scatter plot indicates a relatively weak negative linear relationship of y with x.
Now, use Box-Cox transformation to create a new variable, ‘z.’ Based on the above data, the best lambda calculated is -0.5670. We will use this lambda value to create a new variable, ‘z.’
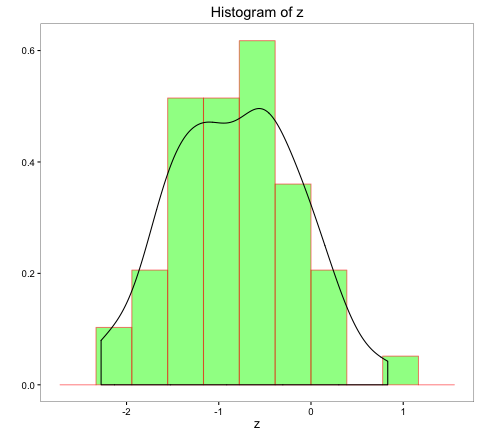
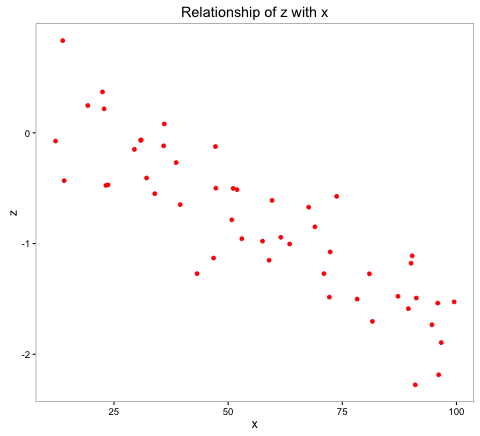
The histogram of z is indicative of normal distribution, and the relationship of z with x is a stronger negative linear relationship.
Linear Regression Model Summary
| Independent Variable | Dependent variable: | |
|---|---|---|
| y | z | |
| x | -0.011522*** | -0.022611*** |
| Constant | 1.291655 | 0.467314 |
| Adjusted R2 | 0.4368 | 0.7584 |
* p < 0.05; ** p < 0.01; *** p < 0.001
There seems to be a substantial improvement in Adjusted R2 from 0.437 to 0.758 with the dependent variable ‘z’ compared to ‘y’. Box-Cox transformation, in the example, led to a huge improvement in the model. Though Box-Cox transformations are immensely useful, they shouldn’t be used indiscriminately. Sometimes, we may not be able to achieve normality in data even after using Box-Cox transformation, and any such transformed data should be thoroughly checked for normality.
v) Missing Data
For an analyst, missing data is one of the most excruciating pain points, as complete data is such a rarity. More often than not, even after trying to exhaust all possible avenues to get the actual values, one is still left with missing values. In such cases, it is better to infer the missing values unless the cost of inferring such values is high or it constitutes a very small fraction of data like say 1%.
Let’s look at an example to understand the importance of inferring missing values. This is an abridged version of the article, which originally appeared here. With the information on Visits, Transactions, Operating Systems, and Gender, we need to build a model to predict Revenue. The summary of the data is given below:
First 5 rows
| Visits | Transactions | OS | Gender | Revenue |
|---|---|---|---|---|
| 7 | 0 | Android | Male | 0 |
| 20 | 1 | iOS | NA | 577 |
| 22 | 1 | iOS | Female | 850 |
| 24 | 2 | iOS | Female | 1050 |
| 1 | 0 | Android | Male | 0 |
Data Summary
| Visits | Transactions | OS | Gender | Revenue |
|---|---|---|---|---|
| Min.: 0.00 | Min.:0.000 | Android:16028 | Female: 2670 | Min.: 0.0 |
| 1st Qu.: 6.00 | 1st Qu.:1.000 | iOS: 6772 | Male:14730 | 1st Qu.: 170.0 |
| Median:12.00 | Median:1.000 | NA: 5400 | Median: 344.7 | |
| Mean:12.49 | Mean:0.993 | Mean: 454.9 | ||
| 3rd Qu.:19.00 | 3rd Qu.:1.000 | 3rd Qu.: 576.9 | ||
| Max.:25.00 | Max. :2.000 | Max. :2000.0 | ||
| NA:1800 |
NA = Missing Observations
We have a total of 7200 missing data points (Transactions: 1800, Gender: 5400) out of 22,800 observations. Almost 8% and 24% of data points are missing for ‘Transactions’ and ‘Gender’, respectively.
We will be using a linear regression model to predict ‘Revenue’ by 1) ignoring the missing data and 2) inferring the missing data.
Missing data Inference
i) Impute ‘Gender’ by Decision Tree
There are several predictive techniques, statistical and machine learning, to impute missing values. We will be using Decision Trees to impute the missing values of ‘Gender.’ The variables used to impute it are ‘Visits’, ‘OS’ and ‘Transactions’.
ii) Impute ‘Transactions’ by Linear Regression
Using a simple linear regression, we will impute ‘Transactions’ by including the imputed missing values for ‘Gender’ (imputed from the Decision Tree). The variables used to impute it are ‘Visits’, ‘OS’ and ‘Gender’.
Now that we have imputed the missing values, we can build the linear regression model and compare the results of the model built by ignoring the missing value and by inferring the missing values.
Linear Regression Model Summary
| Independent Variable | Dependent variable: Revenue | |
|---|---|---|
| Model A (ignored missing values) | Model B (inferred missing values) | |
| Transactions | 418.273*** | 405.619*** |
| OS: iOS | 243.864*** | 243.300*** |
| Gender: Male | -238.319*** | -240.786*** |
| Constant | 171.883*** | 186.184*** |
| Observations | 15,600 | 22,800 |
| Adjusted R2 | 0.719 | 0.776 |
* p < 0.05; ** p < 0.01; *** p < 0.001
‘Visits’ is not included in the models since the variable is statistically insignificant at the 5% significance level. It is clearly evident from the above table that Model B is much better compared to Model A since the Adjusted R2 is much better.
Imputation of missing values is a tricky subject and unless the missing data is not observed completely at random, imputing such missing values by a Predictive Model is highly desirable since it can lead to better insights and overall increase in performance of your predictive models.
vi) Dummy Variables
When dealing with nominal categorical variables with more than 2 levels, like the levels in an Operating System, it is better to create dummy variables, i.e., different variables for each level. This way, you would get a different coefficient or multiplier factor for each level and not suffer from assuming any order in the attribute/levels in the categorical variable. In order to not create redundancy in data, the trick is to create one dummy variable less than the levels in the categorical variable.
In the trick discussed to bin numerical to variable (part 2), we built a better model by binning the numerical variable ‘Age’. We can improve the model further by creating a dummy variable for the ‘Age Group’ and leaving out the statistically insignificant variable, if any.
Logistic Regression Model Summary
| Independent Variable | Dependent variable: Interact | |
|---|---|---|
| Model A – Without Dummy | Model B – With Dummy | |
| Age | -0.062* | -0.03776** |
| Age Group: ≥21 & < 42 | 1.596* | |
| Age Group: > 42 | 1.236 | |
| OS: iOS | 2.534*** | |
| ≥21 & < 42 (Dummy) | 1.05887* | |
| iOS (Dummy for OS) | 2.40673*** | |
| Constant | 0.696 | 0.46429 |
| Observations | 165 | 165 |
| Residual Deviance | 149.93 | 150.97 |
| AIC | 159.93 | 158.97 |
* p < 0.05; ** p < 0.01; *** p < 0.001
Instead of using the categorical variable ‘Age Group,’ we have created 2 new variables, ‘>= 21 & < 42’ and ‘>= 42’. We don’t need to create the variable ‘< 21’ since if the data indicates the user is not in the age group >= 21 & <42 and >= 42, then the user is < 21.
If you look closely at the coefficients, you will notice that the users in the age group >= 42 have a positive coefficient with ‘Interact,’ i.e., users in that age group have a higher probability of interacting compared to the base-level users in the age group < 21. This seems counter-intuitive as the users who interacted with the app reduced substantially for users >= 42 years, as can be seen from the table below:
| < 21 | ≥ 21 & < 42 | ≥ 42 | |
|---|---|---|---|
| 0 | 10 | 22 | 33 |
| 1 | 31 | 60 | 9 |
This shortcoming is addressed in the model built with dummy variables. Dummy variables created for users in the age group >= 42 are not included in Model B since it is statistically insignificant.
Let’s look at another example where the task is to predict ‘Revenues’ from ‘Gender’, ‘OS’, ‘Visits’ and ‘Age Group’.
First 5 rows
| Gender | OS | Visits | Age Group | Revenue |
|---|---|---|---|---|
| Male | Android | 6 | B | 130.45 |
| Female | Android | 7 | D | 79.86 |
| Male | Windows | 12 | B | 398.17 |
| Female | iOS | 8 | D | 221.91 |
| Female | Windows | 8 | D | 114.27 |
Data Summary
| Gender | OS | Visits | Age Group | Revenue |
|---|---|---|---|---|
| Female: 29 | Android: 29 | Min.: 1.0 | A: 26 | Min. : 0.0 |
| Male: 71 | Windows: 38 | 1st Qu.: 6.00 | B: 27 | 1st Qu.: 134.0 |
| iOS: 33 | Median: 8.00 | C: 20 | Median: 201.7 | |
| Mean: 7.79 | D: 27 | Mean: 219.6 | ||
| 3rd Qu.: 10.00 | 3rd Qu.: 291.7 | |||
| Max. : 14.00 | Max. : 527.9 |
We will build 2 models: Model A – No Dummy Variables for ‘OS’ and ‘Age Group’ and Model B -Dummy Variables for ‘OS’ and ‘Age Group’.
Linear Regression Model Summary
| Independent Variable | Dependent variable: Revenue | |
|---|---|---|
| Model A – Without Dummy | Model B – With Dummy | |
| Visits | 33.1408*** | 33.057*** |
| Gender: Male | 58.983*** | |
| OS: Windows | 3.945 | |
| OS: iOS | 111.662*** | |
| Age Group: B | 47.081*** | |
| Age Group: C | -2.332 | |
| Age Group: D | -61.1*** | |
| iOS (Dummy for OS) | 107.660*** | |
| B (Dummy for AgeGroup) | 47.085*** | |
| Constant | -72.979*** | -128.079*** |
Adjusted R2 | 0.885 | 0.8868 |
* p < 0.05; ** p < 0.01; *** p < 0.001
The Adjusted R2 has shown a slight improvement for Model B, but more importantly, Model B requires less variable information than Model A.
Dummy variables are useful since they could improve the model’s robustness by reducing the risk of overfitting. This is possible due to the lower number of variables required for building the model while maintaining or improving the model performance.
vii) Interaction
A typical linear regression assuming we have 2 independent variables is of the form:
y=a+1 . x1+ 2 . x2
where y = dependent variable, x1 & x2 = independent variables , β1= coefficient for x1 and β2= coefficient for x2
Each coefficient indicates the effect of the corresponding independent variable on the dependent variable while keeping all other variables constant. But what if we want to understand the effect of 2 or more independent variables on the dependent variable jointly? We can achieve this by adding an interaction term as shown below:
y=a+1 . x1+ 2 . x2+ 3 . x1 . x2
where β3 = coefficient for interaction term x1 . x2
Let’s look at the same binning example to understand the interaction. We will build our model by adding an interaction term with Age and OS and compare it with the default model.
Logistic Regression Model Summary
| Independent Variable | Dependent variable: Interact | |
|---|---|---|
| Model A – Without Interaction | Model B – With Interaction | |
| Age | -0.049*** | -0.02708. |
| OS: iOS | 2.150*** | 8.14033** |
| OS iOS: Age (Interaction Term) | -0.20189* | |
| Constant | 1.483** | 0.65684 |
| Observations | 165 | 165 |
Residual Deviance | 157.2 | 144.77 |
AIC | 163.2 | 152.77 |
* p < 0.05; ** p < 0.01; *** p < 0.001; . p < 0.1
Model B has shown a good improvement with the interaction term over Model A, as observed from the lower Residual Deviance and AIC. It shows that Age, jointly with OS, shows a statistically significant relationship with Interact.
In this part, we have looked at the tricks iv to vii in detail. The ensuing part will discuss tricks viii and ix in detail.
Jacob Joseph 
Heads Data Science.Expert in AI, Data & Analytics and awarded 40 under 40 Data Scientists in India.
Free Customer Engagement Guides
Join our newsletter for actionable tips and proven strategies to grow your business and engage your customers.